我们来讲讲树状数组和线段树的原理和应用

那么，这有个问题：

如题，已知一个数列，你需要进行下面两种操作：

1.将某一个数加上x

2.求出某区间每一个数的和

那么，如果是一般人，就会拿一维数组存储区间。当然，一维数组可以做到O(1)的修改，但是，区间查询的复杂度会高达O(y-x)！（我们要查询x，y的区间和）

所以，我们这个时候要用到树状数组

那么，什么是树状数组呢？我们给个图感性理解一下:

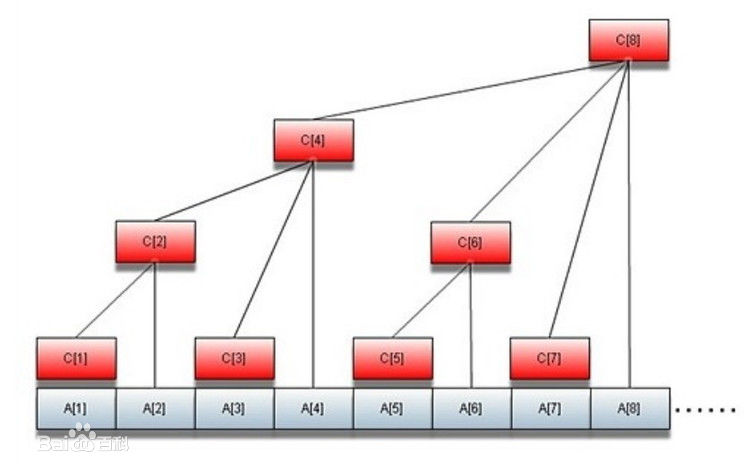
我们每次输入a[]，然后c数组就会存储一个或多个a数组的和，所以就可以轻松做到区间查询

可以看出，这里是有个规律的

c[1]=a[1]
c[2]=a[1]+a[2]
c[3]=a[3]
c[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=a[5]+a[6]
c[7]=a[7]
c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]

那么，这里有个有意思的性质，也就是这个隐藏的规律：

1
2
3

1&-1=001&111=001=1
2&-2=010&110=010=2
3&-3=011&101=001=1

显然，这里c数组与a数组的存储关系可以用二进制表示，所以我们就可以写一个$lowbit$

1
2
3

inline int lowbit(int x){//inline只是个常数优化而已，不加也行
	return x&-x;
}

然后我们就要区间修改，那么，我们先一步一步想：

a[1]会被c[1],c[2],c[4],c[8]几个点储存，我们可以看出，除了c[1]之外，都满足$2^n$且$n\ge 1$

也就是说，除了第一个数组以外，都是2的n次方

我们继续往下分析，都可以得到这个结论

那么，我们就可以这么写：

void change(int v,int x){//v表示在这个数在区间的位置，x表示这个数
    while(v<=n){
        c[v]+=x;//每个跟a[v]的数有关系的c数组都加上x
        v+=lowbit(v);//访问下一个跟a[v]有关系的c数组
    }
}

然后我们就完成了树状数组的构造啦！

最后，还有一个问题：怎么进行区间查询？

那么，想一下朴素的前缀和做法的区间和怎么求

是不是要定义一个数组sum，然后可以求出sum[n]=a[1]+a[2]+……+a[n]
(注意：这里前缀和是求1-n的区间和)

那么，我们可以发现：

sum[1]=a[1]
sum[2]=a[1]+a[2]
sum[3]=a[1]+a[2]+a[3]
sum[4]=a[1]+a[2]+a[3]+a[4]
c[1]=a[1]
c[2]=a[1]+a[2]
c[3]=a[3]
c[4]=a[1]+a[2]+a[3]+a[4]

然后经过显然分析之后，我们可以发现：

sum[1]=c[1]
sum[2]=c[2]
sum[3]=c[3]+c[2]
sum[4]=c[4]

这里的$=$是计算机意义上的$==$

然后，我们继续发现：

sum[1]=c[1]+c[0]
sum[2]=c[2]+c[0]
sum[3]=c[3]+c[2]
sum[4]=c[4]+c[0]

也就是：

sum[1]==[1]+c[1-lowbit(1)]
sum[2]=c[2]+c[2-lowbit(2)]
sum[3]=c[3]+c[3-lowbit(3)]
sum[4]=c[4]+c[4-lowbit(4)]

所以我们就可以写出区间查询的操作啦！

注意：树状数组的区间查询只能做到1到n的区间和，所以当我们要查询x到y的的区间和的时候要先求出1到y的区间和，再减去1到x-1的区间和(到x-1是因为要包括x)

long long getans(int x){
    long long ans=0;
    while(x){
        ans+=c[x];//ans从x加到1
        x-=lowbit(x);//访问下一个c数组
    }
    return ans;
}

这样，我们的树状数组就结束啦

其实，树状数组的代码很简单，就是理解起来很吃力，我们完全可以背代码

树状数组其实不好讲，很多人可能看了我写的还是有点懵，可以先跟着写一下代码，自己慢慢理解

给你们模版：树状数组

再给一下~~高清无码~~的代码：

#include<cstdio>
using namespace std; 
int n,m;
int c[1000001];
int lowbit(int x){
    return x&-x;
}
void change(int v,int x){
    while(v<=n){
        c[v]+=x;
        v+=lowbit(v);
    }
}
long long getans(int x){
    long long ans=0;
    while(x){
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        int a;
        scanf("%d",&a);
        change(i,a);
    }
    for(int i=1;i<=m;i++){
        int k,a,b;
        scanf("%d%d%d",&k,&a,&b);
        if(k==1){
            change(a,b);
        }
        else printf("%lld\n",getans(b)-getans(a-1));
    }
    return 0;
}

树状数组还能用差分做到区间修改(一段区间加上一个数)和单点查询(查询一个点的值)

说完树状数组，我们再来谈谈线段树

先说线段树的用途：

线段树是一个支持区间修改，区间查询的强大的数据结构。虽然那两个树状数组也可以做到，但是代码实现却比较麻烦

树状数组是不好理解，代码好写；反之，线段树是好理解，代码不好写

线段树的复杂度比树状数组能高一点点，所以在下面的代码中，我会带一点位运算和一些常数优化的骚操作

那么，线段树长什么样子，~~好吃吗？~~

这个就是线段树：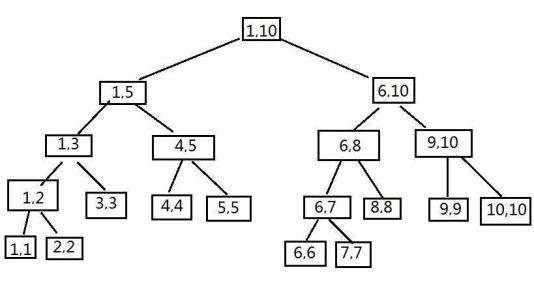

这个是存储1-10区间的线段树

我们可以发现，线段树是个二叉树，所以它有二叉树的性质，左儿子的编号是$x2$，右儿子的编号是$x2+1$

所以我们可以写出以下代码：

inline int ls(int x){
	return x<<1;//在这里x<<1等于x*2
}
inline int rs(int x){
	return x<<1|1;//在这里x<<1|1相当于x*2+1
}

在这里，给大家科普一下：每左移一位就是乘上2，每右移一位就是/2，然后在上面|1就相当于+1

注：inline 可以加在非递归函数前面，可以防止无效数据进入，在递归函数中inline无效，而且可能会报错

那么，线段树是怎么储存的呢？

线段树主要运用二分的思想。因为是二叉树，所以,除非没有子节点，每个节点都有两个子节点。所以，每一个区间都可以是被二分的形式储存。比如，一个储存1-4区间和的节点的两个子节点就会分别储存1-2，2-4

先看一张线段树的节点关系图：

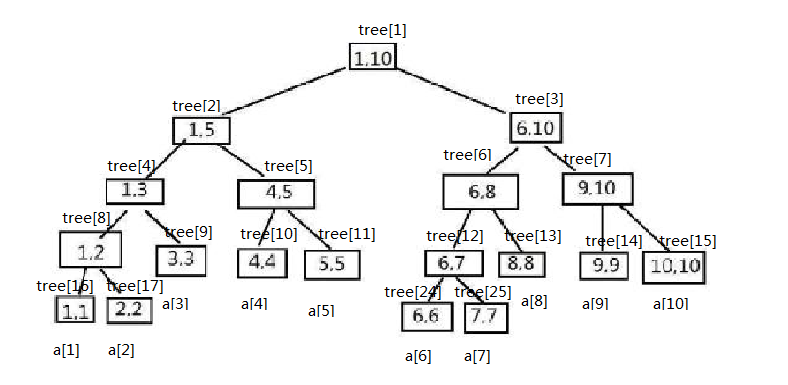
这个图很好理解，然后我们就可以发现一个逻辑关系：

tree[1]=tree[2]+tree[3]//说明：tree[1]存储1-10，tree[2]存储1-5，tree[3]存储6-10，所以tree[1]就可以看作是存储tree[2]+tree[3]
tree[2]=tree[4]+tree[5]
tree[3]=tree[6]+tree[7]
···

这个储存的规律也是很明显了，就是：

inline void push_up(int x){
    ans[x]=ans[ls(x)]+ans[rs(x)];
}
//个人习惯，下面的tree都用ans替代

那么，我们写这个函数是为了以后的建树和区间修改操作都维持一个逻辑关系，就是父节点等于两个子节点的和，还告诉我们父节点维护的区间和是它的左儿子和右儿子维护的区间的总区间，不过这个逻辑关系也可以是子节点的最小值等(具体看题目的要求)

那么我们就开始建树：

void build(int x,int l,int r){
    if(l==r){
        ans[x]=a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(ls(x),l,mid);
    build(rs(x),mid+1,r);
    push_up(x);
}

那么，很多人应该会问：$l==r$的一系列语句是干什么的

答：因为整个建树操作是以二分的方式进行的，那么

这个图已经很清楚了，我们可以看到在那些没有子节点的节点上只储存了一个单点，也就是相当于储存了一个区间，且左边界=右边界。所以我们就可以判断，如果一个节点的左右边界相等，也就是说明已经二分到一个数了，这个节点没有子节点，那么ans数组就存储a数组，在上面$ans[x]=a[l]$是存储l边界的数，其实储存$a[r]$也可以，因为$l==r$

那么，建树应该就没什么问题了吧？毕竟这个很好理解

建树之后就是区间修改

在这里我就不讲单点修改了，因为这个树状数组就可以做到了，没有必要在线段树里面实现

那么，这里我们就要引入一个概念——懒标记

那么，我们修改线段树是从上而下修改的，如果我们把需要修改的节点全都标记上去，那么复杂度会增大，线段树的优势就荡然无存，所以我们就要用到懒标

懒标记的作用是记录每次、每个节点要更新的值，也就是$delta$,但线段树的优点不在于全记录（全记录依然很慢qwq），而在于传递式记录：

整个区间都被操作，记录在公共祖先节点上；只修改了一部分，那么就记录在这部分的公共祖先上；如果四环以内只修改了自己的话，那就只改变自己。

——_皎月半洒花

引用某大佬的解释，这就是懒标

简单说，就是我们在一个需要更新的节点上打上标记，代表这个节点要加上的数，后面每次访问到这个节点，就把节点往下移一位就行了

对，这就是懒标的运行方式，所以我们就需要把节点的标记等信息往下传，于是我们就可以写出$push_ down$了

inline void f(int x,int l,int r,int k){
    tag[x]+=k;
    ans[x]+=k*(r-l+1);//因为是区间的修改，所以ans数组加上k要加区间的长度次
}
inline void push_down(int x,int l,int r){
    int mid=(l+r)>>1;
    f(ls(x),l,mid,tag[x]);
    f(rs(x),mid+1,r,tag[x]);
    tag[x]=0;
}

f函数的目的，其实就是为了记录当前节点所代表的区间，其实我们可以不写f函数，但是那样代码会难看很多，而且写起来很不舒服

写完懒标，我们就来开始写区间修改

void update(int now_l,int now_r,int l,int r,int x,int k){
    if(now_l<=l&&r<=now_r){//如果这个区间完全被覆盖
        f(x,l,r,k);
        return;
    }
    push_down(x,l,r);
    ll mid=(l+r)>>1;
    if(now_l<=mid)update(now_l,now_r,l,mid,ls(x),k);
    if(mid<now_r)update(now_l,now_r,mid+1,r,rs(x),k);
    push_up(x);
}

那么，now_l和now_r是来表示进行修改的区间。我们在往下递归的之前先下传递修改，然后我们回溯之后再用子节点的信息维护父节点

之后呢，我们就来看一下区间查询

这个查询跟上面一样，都是用到分块的思想，所以思路都差不多

int query(int ask_l,int ask_r,int l,int r,int x){
    int res=0;
    if(ask_l<=l&&r<=ask_r){//完全被覆盖就返回此处的值
        return ans[x];
    }
    push_down(x,l,r);
    int mid=(l+r)>>1;
    if(ask_l<=mid)res+=query(ask_l,ask_r,l,mid,ls(x));
    if(mid<ask_r)res+=query(ask_l,ask_r,mid+1,r,rs(x));
    return res;
}

提示：区间查询是不会修改任何值，所以这里就不需要用到$push_ up$了

那么，我们就写完线段树辣！

给你们模板线段树1

再加上代码：
(这里的模板要求我们用到long long，所以我就把int都改成了long long)

#include<cstdio>
#define ll long long
using namespace std;
const int MAXN=100001;
ll n,m;
ll a[MAXN],tag[MAXN<<2],ans[MAXN<<2];//这里的ans和tag都开了四倍，可以自己手推，就会发现不开四倍会超空间
inline ll ls(ll x){
    return x<<1;
} 
inline ll rs(ll x){
    return x<<1|1;
}
inline void push_up(ll x){
    ans[x]=ans[ls(x)]+ans[rs(x)];
}
void build(ll x,ll l,ll r){
    if(l==r){
        ans[x]=a[l];
        return;
    }
    ll mid=(l+r)>>1;
    build(ls(x),l,mid);
    build(rs(x),mid+1,r);
    push_up(x);
}
inline void f(ll x,ll l,ll r,ll k){
    tag[x]+=k;
    ans[x]+=k*(r-l+1);
}
inline void push_down(ll x,ll l,ll r){
    ll mid=(l+r)>>1;
    f(ls(x),l,mid,tag[x]);
    f(rs(x),mid+1,r,tag[x]);
    tag[x]=0;
}
void update(ll now_l,ll now_r,ll l,ll r,ll x,ll k){
    if(now_l<=l&&r<=now_r){
        f(x,l,r,k);
        return;
    }
    push_down(x,l,r);
    ll mid=(l+r)>>1;
    if(now_l<=mid)update(now_l,now_r,l,mid,ls(x),k);
    if(mid<now_r)update(now_l,now_r,mid+1,r,rs(x),k);
    push_up(x);
}
ll query(ll ask_l,ll ask_r,ll l,ll r,ll x){
    ll res=0;
    if(ask_l<=l&&r<=ask_r){
        return ans[x];
    }
    push_down(x,l,r);
    ll mid=(l+r)>>1;
    if(ask_l<=mid)res+=query(ask_l,ask_r,l,mid,ls(x));
    if(mid<ask_r)res+=query(ask_l,ask_r,mid+1,r,rs(x));
    return res;
}
int main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
    }
    build(1,1,n);
    for(int i=1;i<=m;i++){
        int c;
        scanf("%d",&c);
        if(c==1){
            ll x,y,k;
            scanf("%lld%lld%lld",&x,&y,&k);
            update(x,y,1,n,1,k);
        }
        if(c==2){
            ll x,y;
            scanf("%lld%lld",&x,&y);
            printf("%lld\n",query(x,y,1,n,1));
        }
    }
    return 0;
}

浅谈线段树和树状数组